Time derivative of the Keplerian function

I started experimenting with the automatic differentiation package autograd and, wow this thing is pretty amazing!

From the tutorial, we can see what it does and how it works:

Autograd takes in a function, and gives back another function that computes its derivative.

sounds simple…

Autograd works on ordinary Python and Numpy code containing all the usual control structures, including while loops, if statements, and closures.

that’s cool!

To compute the gradient, autograd first has to record every transformation that was applied to the input as it was turned into the output of your function.
(…) autograd wraps functions so that when they’re called, they add themselves to a list of operations performed.
After the function is evaluated, autograd has a list of all operations that were performed and which [variables] they depended on. This is the computational graph of the function evaluation. To compute the derivative, we simply apply the rules of differentiation to each node in the graph

Ok, let’s try it out!

The Keplerian function

When we’re trying to detect an exoplanet using radial-velocity (RV) measurements, we have to “fit” a Keplerian function to a timeseries. The function (of time) looks like this

The parameters \(K\), \(\omega\), and \(e\) are the semi-amplitude, argument of periastron, and eccentricity of the exoplanet’s orbit. The function \(f(t)\) is called the true anomaly, and it’s actually a complicated function of time, which depends on two other parameters: the orbital period \(P\) and the time of periastron \(T_0\).

Below is a simple Python implementation of the Keplerian function:

import numpy as np

def keplerian_1planet(time, P, K, ecc, omega, T0):
    M = 2. * np.pi * (time-T0) / P
    E = ecc_anomaly(M, ecc)
    nu = true_anomaly(E, ecc)
    vel = K * (np.cos(omega+nu) + ecc*np.cos(omega))
    return vel

def true_anomaly(E, e):
    return 2. * np.arctan( np.sqrt((1.+e)/(1.-e)) * np.tan(E/2.))

def ecc_anomaly(M, e):
    E0 = M; E = M
    for _ in xrange(200):
        g = E0 - e * np.sin(E0) - M
        gp = 1.0 - e * np.cos(E0)
        E = E0 - g / gp
        if (np.linalg.norm(E - E0, ord=1) <= 1.234e-10): 
            return E
        E0 = E
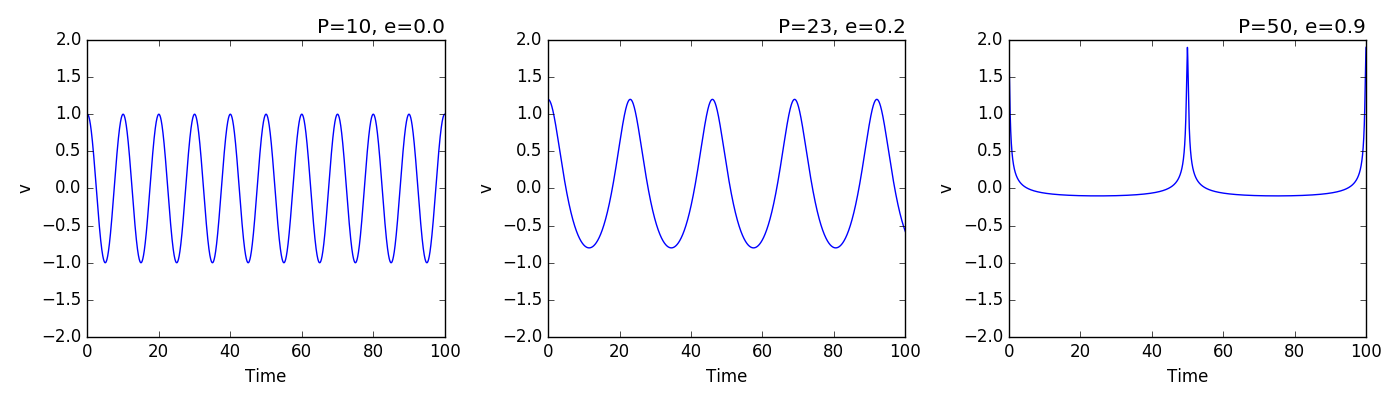
    return E

which can produce RV curves like this:

The time derivative

Ok, so the next question clearly is:
can we use autograd to calculate the derivative of the Keplerian function with respect to time?

Well, yes of course!

In the code above substitute
import numpy as np
with
import autograd.numpy as np

Then, fix the parameters and create a function of time only

P, K, e, w, T0 = 10., 1., 0.1, 0., 0.
kep = lambda t: keplerian_1planet(t, P, K, e, w, T0)

Now we can use the elementwise_grad function to calculate the derivative:

from autograd import elementwise_grad
kepp = elementwise_grad(kep)

That’s it!!

wrap up

Compute automatic derivatives of your Python functions with autograd!
Use

import autograd.numpy as np
from autograd import grad, elementwise_grad
# for scalar and vector-valued functions, respectively

Let me know in the comments if this is helpful, wrong or super-duper cool.